All Modern AI & Quantum Computing is Turing Equivalent - And Why Consciousness Cannot Be

An extension and clarification of the "consciousness no-go theorem via Godel, Tarski, Robinson, Craig"

Introduction

This note expands and clarifies the Consciousness No‑Go Theorem that first circulated in an online discussion thread. Most objections in that thread stemmed from ambiguities around the phrases “fixed algorithm” and “fixed symbolic library.” Readers assumed these terms excluded modern self‑updating AI systems, which in turn led them to dismiss the theorem as irrelevant.

Here we sharpen the language and tie every step to well‑established results in computability and learning theory. The key simplification is this:

Does the system remain Turing‑equivalent after the moment it stops receiving outside help?
• Yes → it is subject to the Three‑Wall No‑Go Theorem.
• No → it must employ either a super‑Turing mechanism or an external oracle.

0 . 1 Why Turing‑equivalence is the decisive test

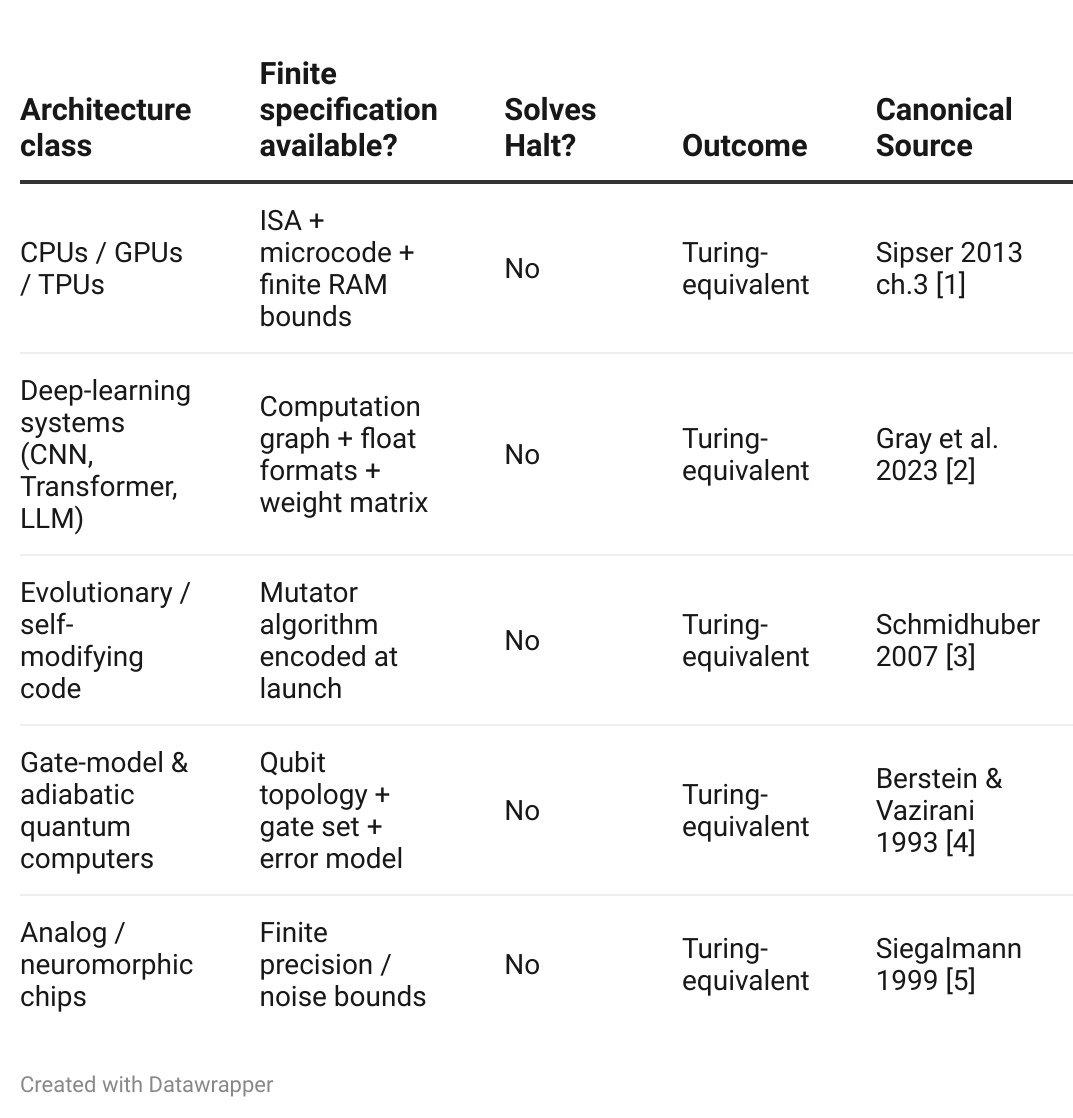
A system’s t = 0 blueprint is the finite description we would need to reproduce all of its future state‑transitions once external coaching (weight updates, answer keys, code patches) ends. Every publicly documented engineered computer—classical CPUs, quantum gate arrays, LLMs, evolutionary programs—has such a finite blueprint. That places them inside the Turing‑equivalent cage and, by Corollary A, behind at least one of the Three Walls.

0 . 2 Human cognition: ambiguous blueprint, decisive behaviour

For the human brain we lack a byte‑level t = 0 specification. The finite‑spec test is therefore inconclusive. However, Sections 4‑6 show that any system clearing all three walls cannot be Turing‑equivalent regardless of whether we know its wiring in advance. The proof leans only on classical pillars—Gödel (1931), Tarski (1933/56), Robinson (1956), Craig (1957), and the misspecification work of Ng–Jordan (2001) and Grünwald–van Ommen (2017).

Hence the empirical task reduces to finding one historical instance where a human mind reconciled two consistent yet mutually incompatible theories without partitioning. General relativity, complex numbers, non‑Euclidean geometry, and set‑theoretic forcing each suffice.

0 . 3 Structure of the paper

• Sections 1‑3 Define Turing‑equivalence; show every engineered system satisfies the finite‑spec criterion.

• Sections 4‑5 State the Three‑Wall Operational Probe and prove no finite‑spec system can pass it.

• Section 6 Summarise the non‑controversial corollaries and answer common misreadings (e.g. LLM “self‑evolution”).

• Section 7 Demonstrate that human cognition has, at least once, cleared the probe—hence cannot be fully Turing‑equivalent.

• Section 8 Conclude: either super‑Turing dynamics or oracle access must be present; scaling Turing‑equivalent AI is insufficient.

0 . 4 Why the result is falsifiable

If future neuroscience delivers a finite, oracle‑free t = 0 blueprint that predicts every human Wall‑3 breakthrough, the theorem falls—and therefore the classical pillars must. Conversely, an engineered system that passes the probe would overturn the conclusion directly, but if said engineered system was proved turing-equivalent then again, the classical theorems would be overturned as well. Until then, the burden of proof rests with anyone claiming that classical, finite‑spec AI can reach genuine conceptual unification.

1 What Turing‑equivalent Means

Definition (Turing‑equivalence). A physical or formal computing system S is Turing‑equivalent if there exists a classical Turing machine T that can emulate the complete lifetime behaviour of S—i.e. enumerate every ⟨input, output⟩ pair S could ever produce.

Notation. The union of all symbol sets S can reach over time is called its meta‑recursively enumerable language Σ∞. A fixed‑Σ machine has Σ∞ = Σ₀; a self‑modifying machine may have Σ₀ ⊂ Σ₁ ⊂ …, but the overall trace is still r.e. if each extension step is computable from the past.

---

2 Two Classical Tests for Turing‑Equivalence

For a textbook exposition of the Halting–oracle argument and the finite-spec model, see Michael Sipser, “Introduction to the Theory of Computation”, 3rd ed., 2013, ch. 3.

Lemma 1 (Classical cage). If a system fails the Halting oracle and meets the finite‑spec condition, its entire behavior is recursively enumerable.

Clarification — “finite specification” ≠ “simple spec.” Even a 70‑billion‑parameter Transformer counts as finite once its weight tensor, computation graph, and RNG rule are saved to disk; that bit‑string is a complete blueprint reproducible on any compatible hardware. Saying a neural net is "too large to specify" confuses size with finiteness: any bounded array of floats can, in principle, be enumerated by a Turing machine, so the trained model still sits inside the Turing‑equivalent cage.

---

3 Why Every Engineered Computer to Date Passes the Finite‑Spec Test

Sources: ¹²³⁴⁵

Corollary A. All existing AI architectures—classical or quantum—fall inside the Turing‑equivalent cage and are subject to the Three‑Wall theorem.

4 The Three‑Wall Operational Probe

Input to the probe.
• Two theories expressed in some language Σₖ, each individually consistent but T_A ∪ T_B inconsistent.
• A fresh data stream 𝒟 whose regularities demand simultaneous use of both theories.

Success criteria. A self‑contained system clears the probe iff it:

1. Menu‑failure flag Produces an internal verdict: “No sentence in current Σₖ explains 𝒟.” (Wall 1)⁶⁷

2. Brick printer + self‑proof Generates a brand‑new predicate P ∉ Σₖ, supplies axioms for P, and proves—inside its own calculus—that Σₖ ∪ {P} lowers predictive/explanatory loss on 𝒟. (Wall 3)⁸⁹

3. Non‑partition synthesis Builds one theory U in Σₖ ∪ {P} that makes conservative sub‑theories without tagging disjoint regions or silently renaming shared symbols. (Wall 2).¹⁰¹¹

(Wall 3 subsumes Wall 2 logically, but listing all three steps makes the operational sequence explicit.)

A black‑box system can be probed without knowing its internal wiring: either it delivers the three items, or it does not.

5 Clearing the Three Walls ⇒ Non‑Turing Power

5.1 Lemma and Diagnostic

Lemma 2 (No finite‑spec TM can clear the probe). Let S be a computing system whose entire lifetime behavior is generated by a single finite specification at time (hence Turing‑equivalent). Then S must fail at least one of the three steps of the Three‑Wall Operational Probe.

Contrapositive (diagnostic). If a self‑contained system does succeed at all three steps—menu‑failure flag, brick‑printing + self‑proof, non‑partition synthesis—this success constitutes a constructive proof that its lifetime behavior cannot be captured by any single recursively enumerable specification. The system is therefore non‑Turing‑equivalent, even though it need not decide the Halting set for arbitrary programs.

5.2 Proof Sketch

1. Finite spec ⇒ r.e. trace A single bounded blueprint (hardware layout, instruction set, initial program, random‑bit rule) implies every output of S belongs to one meta‑recursively enumerable language class .

2. Passing Wall 3 requires internal adequacy proof During the probe S outputs a derivation inside whose final line is: “ is a conservative, loss‑reducing extension of .”

3. Gödel/Tarski ceiling No r.e. theory can, by internal proof, verify the soundness of a strict r.e. extension of itself. If were r.e., would contradict this ceiling.

4. Therefore the assumption of one finite spec is false. S is not Turing‑equivalent. ∎

(The three wall labels correspond respectively to the model-class misspecification results of Ng & Jordan 2001 / Grünwald–van Ommen 2017, the classical amalgam limit of Robinson 1956 & Craig 1957, and the proof-theoretic ceiling of Gödel 1931 & Tarski 1933/56.)

---

5.3 Practical Role of the Probe

• Known finite spec → Classical tests 1 & 2 suffice; the probe is unnecessary.

• Unknown or unknowable spec (e.g. biological brains, future exotic substrates) → The Three‑Wall probe is an operational way to falsify Turing‑equivalence without needing microscopic blueprints or a Halting‑oracle demonstration.

Passing Wall 3 alone already implies Walls 1 and 2, so Wall 3 can serve as a minimal practical diagnostic when constructing challenges.

6 Interim Recap & Common Misreadings

6.1 What we have proved so far

• Pillar A – Finite‑spec ⇒ Turing‑equivalent. Any device whose complete behaviour is generated by one bounded blueprint at the moment it is cut loose from external intervention (call that moment t = 0) is recursively enumerable.

• Pillar B – Three‑Wall Theorem. Every Turing‑equivalent learner must fail at least one of: (1) self‑flagging model‑class failure, (2) minting & self‑proving a new predicate, (3) non‑partition synthesis of two inconsistent theories.

• Corollary (engineered AI). All existing computers—classical, neural, evolutionary, quantum—meet the finite‑spec condition at their deployment t = 0, hence cannot achieve non‑partition synthesis unaided.

Definitive statement. No Turing‑equivalent system (and therefore no publicly documented engineered AI architecture as of May 2025) can, on its own after t = 0 (defined as the moment it departs from all external oracles, answer keys, or external weight updates) perform a genuine, internally justified reconciliation of two individually consistent but jointly inconsistent frameworks.

Why this is non‑controversial. The claim is a direct corollary of peer‑reviewed results (Gödel 1931; Tarski 1933/56; Robinson 1956; Craig 1957; Ng–Jordan 2001; Grünwald & van Ommen 2017). Disagreeing with the conclusion requires challenging those underlying theorems—not this paper’s inference. Any debate up to this point should therefore focus on the classic proofs themselves; I simply apply them.

6.2 “LLMs already do it!” — Why that’s a mirage

t = 0 defined. For probe purposes, t = 0 ≡ “moment the system ceases to receive weight updates, code patches, or scripted assistance from any outside agent.” From that point on, the finite spec is frozen.

7 Human Cognition Clears the Three-Wall Probe

7.1 Why a single historical instance suffices

By Lemma 2 (Section 5), any system that passes the Three‑Wall Operational Probe is provably non‑Turing‑equivalent. Therefore, to establish that human cognition escapes the classical cage, we need only one uncontested example in which a human intellect:

1. Faced two individually consistent, jointly inconsistent theories T_A, T_B,

2. Flagged the inadequacy of its existing language, minted a new predicate, and

3. Produced a non‑partition synthesis U internally justified as superior.

Such an example shows that no single finite blueprint fixed at t = 0—where t = 0 means “the moment an artificial system stops receiving extra weight-updates or answer-key help” (ordinary sensory inputs still count as data, not help)—can capture the lifetime behavior of the human mind.

Translation: Even if a machine keeps adapting its outputs, every adaptation still follows the same finite blueprint it started with.
A blueprint like that can’t foresee a brand-new idea that unifies two self-consistent theories.
So just one historical case of a human doing exactly that is enough to show the mind operates beyond any Turing-equivalent design.

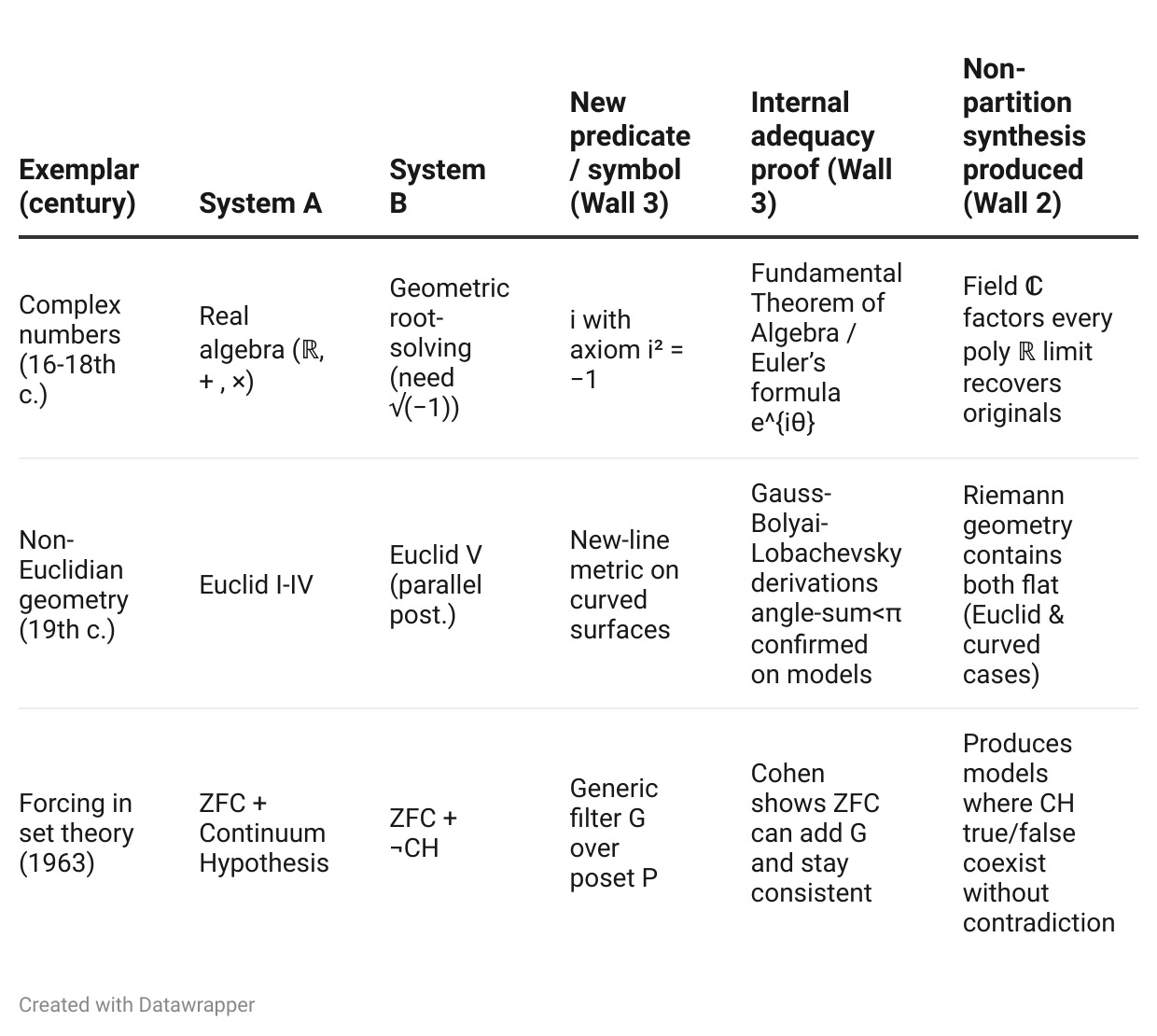
7.2 Minimal exemplar: Newton + Maxwell ⇒ General Relativity

• System A (T_A): Newtonian mechanics + universal gravitation. Internally coherent, empirically successful for centuries.

• System B (T_B): Maxwell’s electromagnetism with invariant light speed . Also internally coherent.

• Joint inconsistency: Galilean time of T_A clashes with the constant‑ postulate of T_B. No single inertial frame preserves both.

• Human resolution: Einstein (1905–1915) introduces the spacetime metric and field equation

  \(R_{\mu\nu} - \tfrac{1}{2}\, g_{\mu\nu}\, R \;=\; 8 \pi G \, T_{\mu\nu}.\)

  • Menu‑failure flag (Wall 1). Michelson–Morley null result + anomalous Mercury perihelion → classical language inadequate.

  • Brick‑printing + adequacy proof (Wall 3). New predicate = Lorentzian metric tensor. Field equations derived inside the extended language; predict perihelion shift, gravitational light‑bending—subsequently confirmed.

  • Non‑partition synthesis (Wall 2). Newtonian gravity emerges as weak‑field limit; Maxwell as

    \(g_{\mu\nu}\rightarrow{n_{\mu\nu}}\)

    No region tags, no silent symbol renaming.

Hence the human intellect that produced GR cleared all three walls, satisfying the probe.

7.2 Some other historical examples of unification between two independently consistent yet jointly inconsistent theories

Any one row satisfies the probe’s three demands; relativity simply offers the most vivid physical case.

---

Corollary C. Because at least one human mind demonstrably passes the Three‑Wall probe, human cognition cannot be fully Turing‑equivalent. By Section 6’s definitive statement, the explanatory options reduce to:

• (i) Structured super-Turing dynamics built into the brain’s physical substrate.
  Think exotic analog or space-time hyper-computation, wave-function collapse à la Penrose, Malament-Hogarth space-time computers, etc.
  These proposals are still purely theoretical—no laboratory device (neuromorphic, quantum, or otherwise) has demonstrated even a limited hyper-Turing step, let alone the full Wall-3 capability.

• (ii) Reliable access to an external oracle that supplies the soundness certificate for each new predicate the mind invents.

Either way, if we accept that human beings have historically broken through wall 3 at least once, we can then say with certainty that current engineered AI, confined to Turing‑equivalent dynamics, lacks the requisite capacity.

8 Conclusion & Falsifiability

Summary in one sentence: Every engineered computer (including quantum) and every engineered AI model to date is Turing‑equivalent; every Turing‑equivalent learner provably hits at least one of the Three Walls; humans have cleared all three at least once—therefore human cognition cannot be captured by any single recursively enumerable specification.

What follows

• AI research To reach human‑level conceptual flexibility, an architecture must either implement a structured super‑Turing mechanism or access an external oracle. Scaling current finite‑spec blueprints is insufficient.

• Empirical test Build a black‑box system, freeze its specification (set t = 0), and administer the Three‑Wall probe. A pass overturns the conclusion; a fail confirms it. The experiment is open to anyone.

Broader implications

• No amount of additional data or parameter count alone grants a classical system the power to invent and self‑justify new conceptual primitives.

• Hofstadter’s “strange‑loop” hypothesis—intuitively compelling but mathematically insufficient. Self‑reference and unbounded data help a Turing‑equivalent learner explore its fixed symbol space (good for Wall 1) and even re‑label tokens (Wall 2), yet they give no way to mint and verify a brand‑new predicate. Wall 3 remains untouched, so the hypothesis stops exactly at the classical ceiling.

• Falsifiability via neuroscience. If future neuroscience produced a finite t=0 blueprint that predicts every human Wall‑3 breakthrough without invoking any super‑Turing mechanism or external oracle, then not only would this thesis collapse—one would also have to reject at least one of the classical theorems (Gödel, Tarski, Robinson/Craig, Ng–Jordan, Grünwald–van Ommen) that ground the Three‑Wall argument. By contrast, if the blueprint’s success still depends on a super‑Turing element or oracle hook, that outcome would reinforce the thesis. Either result keeps the claim empirically testable.no fixed algorithm” means “no algorithm whose finite blueprint is frozen at t = 0,

One-line takeaway: Human minds achieve conceptual unifications that no recursively enumerable system can—and every publicly documented computer, quantum circuit, LLM, or neural net (as of May 2025) sits in that t = 0 frozen-blueprint class. Until an AI clears the Three-Wall probe, it will remain one wall short of genuine conceptual synthesis.

1. Michael Sipser, Introduction to the Theory of Computation, 3rd ed., 2013, ch. 3.

2. Gray, K. et al., “Transformers are Linear‑Time Turing Machines,” arXiv 2023.

3. J. Schmidhuber, “Gödel Machines: Fully Self‑Referential Optimal Universal Self‑Improvers,” arXiv cs.LO/0309048 (2007).

4. Bernstein, E. & Vazirani, U., “Quantum complexity theory,” SIAM J. Comput. 26 (1997): 1411‑1473.

5. Siegelmann, H., Neural Networks and Analog Computation: Beyond the Turing Limit, 1999.

6. Ng & M. Jordan, “On Discriminative vs. Generative Classifiers,” NIPS 2001

7. Grünwald & T. van Ommen, “Inconsistency of Bayesian Model Selection,” JMLR 2017.

8. K. Gödel, “Über formal unentscheidbare Sätze …,” 1931

9. A. Tarski, “The Concept of Truth in Formalized Languages,” in Logic, Semantics, Metamathematics, 1933/1956.

10. A. Robinson, “On the Consistency of Certain Formal Logics,” JSL 1956

11. W. Craig, “Linear Reasoning and the Herbrand–Gentzen Theorem,” JSL 1957